疾病预防控制中心的疫苗功效流行病学无能

在 Covid-19 大流行期间，CDC 科学人员定期利用现有的研究数据来评估当前或最新版本的 Covid-19 疫苗的功效，以降低 Covid-19 检测呈阳性的风险。虽然“检测呈阳性”的事实存在一定争议，因为涉及秘密的 PCR Ct 阈值数字，这使得过去几周内未识别出 Covid-19 的未感染者仍保持检测呈阳性，但我在这里的目的是说明疾病预防控制中心有问题的流行病学方法大大夸大了他们报告的疫苗功效百分比。

对照流行病学研究分为三种且仅有三种基本研究设计。要么对受试者的总样本进行抽样，并对每个受试者的病例状态和以前的暴露状态进行评估（这是一项横断面研究），要么对暴露者样本和未暴露者样本进行跟踪，看看谁成为获得病例和对照（队列研究）或病例样本和对照样本，并对每个受试者过去的暴露状态进行评估——这是病例对照研究。如果队列研究涉及将受试者随机分为暴露组和未暴露组，则这是随机对照试验（RCT），但研究设计仍然是队列。

在横断面研究和队列研究中， 风险 可以通过暴露者中的病例数除以暴露者总数来估计暴露者获得感兴趣结果的可能性（即，成为病例受试者，此处检测呈阳性）。对于未曝光的情况也是如此。有趣的是，这两种风险的比较，即相对风险（RR），是暴露的风险除以未暴露的风险。 RR 估计暴露者与未暴露者相比，风险有多严重。对于疫苗或其他降低风险的暴露，RR 将小于 1.0。

横断面研究和队列研究通过抽样设计，可以根据数据估计 RR。然而，病例对照研究不允许估计结果风险，因为改变样本病例与对照的相对数量会影响风险估计。相反，病例对照研究可以估计 可能性 关注的是结果，而不是风险。例如，事件发生的几率为 2:1。该值不受抽样设计的影响。在病例对照研究中，结果的相对赔率（或赔率比，OR）是通过暴露者的结果赔率除以未暴露者的赔率来估计的。

对于疫苗，其功效估计为 1.0 – RR。对于仅估计 OR 而非 RR 的病例对照研究数据，OR 何时足够准确地近似 RR 以便替换在此公式中？该问题具有超出当前范围的详细流行病学历史，但从最简单的意义上来说，当在人群中病例与对照相比并不常见时，OR 近似于 RR。

现在谈谈疾病预防控制中心及其系统性流行病学错误。在最近的一项分析中， 林克-盖勒斯及其同事 9,222 年 19 月 19 日至 21 年 2023 月 14 日期间，对总共 2024 名符合条件的 Covid-XNUMX 样症状个体进行了采样，这些个体寻求在 CVS 和 Walgreen Co. 药房进行 Covid-XNUMX 检测。他们评估了每个人之前的疫苗接种状况以及阳性结果的测试结果。根据定义，这是一项横断面研究，因为没有对病例和对照的个体数量，或暴露（接种疫苗）和未暴露（未接种疫苗）的个体数量进行采样。仅对受试者总数进行了抽样。

然而，研究人员通过使用一种称为逻辑回归的统计分析方法，根据这些数据估计了 OR，而不是 RR，该方法允许针对各种可能的混杂因素调整 OR。在任何研究设计中使用逻辑回归并获得估计的 OR 都没有问题；问题是在疫苗功效公式 1.0 – RR 中使用 OR 值而不是 RR。由于研究设计是横断面的，研究人员本可以从抽样数量中检查人群中相对病例的发生率，但他们似乎没有这样做。事实上，样本总数为 3,295 例，其中 9,222 例为 36%，这还不足以使用 OR 来替代 RR。对于暴露的受试者 (25%) 和未暴露的受试者 (37%) 来说都是如此。

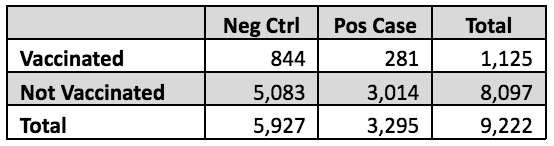
尽管如此，还是可以粗略地了解这种错误的假设对作者声称的 54% 疫苗总体功效有多大影响。下表所示的相关受试者数量在 Link-Gelles 论文的表 1 和表 3 中列出。根据这些原始数据计算 RR 很简单。接种疫苗的风险为 281/1,125 = 25%；在未接种疫苗的人群中，这一比例为 3,014/8,097 = 37%。 RR 是这两者的比率，25%/37% = 0.67，因此基于这些原始数据的疫苗功效将为 1.0 – 0.67 = 0.33 或 33%。

同样，可以根据这些原始数据将 OR 估计为 0.56，如果将其用于疫苗功效公式，则功效为 44%，与使用 RR 正确估计的 33% 功效明显不同。

然而，Link-Gelles 等人。使用从逻辑回归分析中获得的调整后的 OR = 0.46。这与未调整的 OR = 0.56 相差 0.46/0.56 = 0.82。我们可以使用这个调整因子 0.82 来近似估计经过相同因子调整后的原始 RR：0.67*0.82 = 0.55。这些数字如下表所示，表明正确的疫苗功效约为 45%，而不是声称的 54%，并且低于名义上 50% 的期望水平。

作为一名流行病学家，我不清楚为什么我在 CDC 的同事会错误地使用 OR 来替代 RR，因为这种替代所需的假设没有得到满足，并且可以在他们自己的数据中轻松检查。他们在其他地方犯了这个错误（滕福德等人。），疫苗功效也有相当大的差异，大约为 57%，而不是声称的 82%。也许作者认为调整多个混杂变量的唯一方法是使用 OR 的逻辑回归，但用于调整 RR 的相对风险回归早已在各种商业统计分析包中可用，并且很容易实现（杜松).

让我感到惊讶的是，Link-Gelles 和 Tenforde 论文之间的 60 多位作者显然没有一个认识到他们研究的抽样设计是横截面的，而不是病例对照的，因此用于估计的正确参数疫苗功效是 RR 而不是 OR，并且他们的数据不满足用 OR 代替 RR 的罕见疾病假设。因此，这些研究大大高估了其结果中的真实疫苗功效。这不是一个纯粹的学术问题，因为疾病预防控制中心的公共卫生政策决策可以从诸如此类的错误结果中得出。